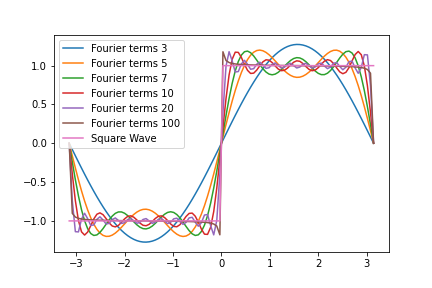
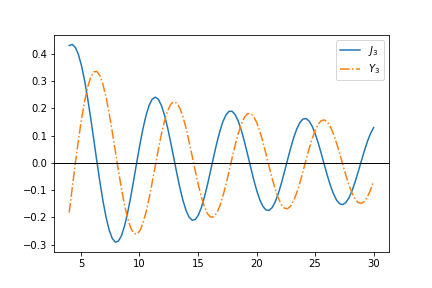
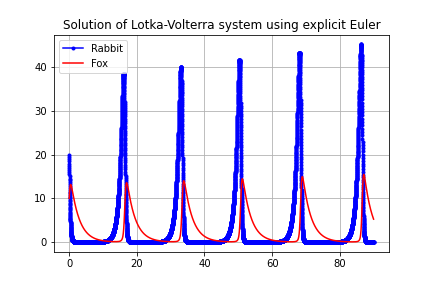
Ordinary Differential Equations

About the course

The construction of mathematical models to address real-world problems has been one of the most important aspects of each of the branches of science. Many mathematical models represented as equations involving functions and their derivatives. Such equations are called differential equations. Equations with one independent variable are called ordinary differential equations. The course will demonstrate the usefulness of ordinary differential equations for modelling physical and other phenomena. Complementary mathematical approaches for their solution will be presented, including analytical methods, graphical analysis and numerical techniques. We will use Python for analysing certain numerical techniques and viewing the solutions of certain equations in an illustrative way.

Course Objectives

• Develop skills in analyzing systems of linear and nonlinear differential equations using analytical and geometrical approaches
• Learn the theoretical aspects of differential equations, including the establishment of existence of solutions, and techniques for obtaining solutions for the various types of ordinary differential equations
• Use the theorems which are especially useful, as they allow one to determine the existence and uniqueness of solutions without having to solve the differential equation
• Understand how to solve system of ordinary differential equations
• Understand how to solve non-autonomous differential equations

Primary Text

• Differential Equations: Theory, Technique, and practice by George F. Simmons and Steven G. Krantz

Other Reference Texts

• Fundamentals of Differential Equations and Boundary Value Problems, Fifth Edition, by Nagle, Saff and Snider
• Differential Equations by Shepley L. Ross
• Nonlinear Ordinary Differential Equations by D. W. Jordan and P. Smith.
• Differential Equations and Dynamical Systems by Perko

Course Material

Python Labs